Example 6: Splitting misfit measurement and model fitting

The example file demo_splitting_misfit.m in the examples/splitting_misfit directory shows how the MSAT function MS_splitting_misfit can be used and plots the value of the misfit function for pairs of splitting parameters. The reference splitting parameters, $\Gamma_1$, for this illustration are $dt_1 = 2$ seconds and $\phi_1 = 0$ degrees. This is compared with $\Gamma_2$ with values varying from $\phi_2 = -90$ to $\phi_2 = 90$ degrees and $dt_2 = 0$ to $dt_2 = 4$ seconds. For the methods that are sensitive to source polarization three values are used, 45, 30 and 0 degrees. The calculation of misfit over this grid of values of $\Gamma_2$ is done as follows in the function calc_misfit_surface:

The call to MS_splitting_misfit calculates the misfit for each of the values of $\Gamma_2$. This is done for each of the polarisation directions and misfit calculation methods ("simple", "intensity", "lam2" and "lam2S") and the calculated misfit surfaces plotted.

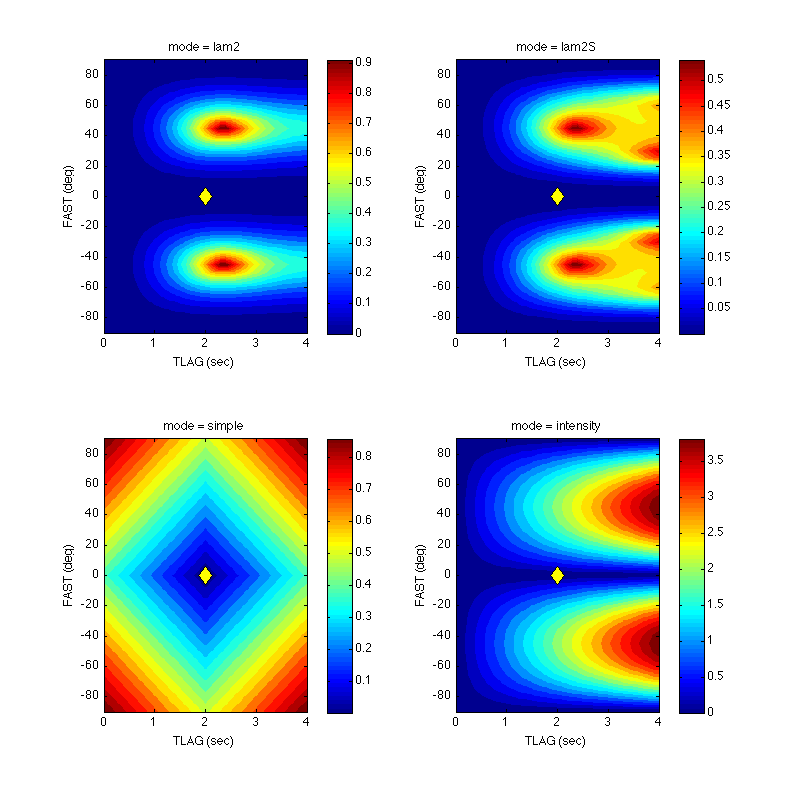
The images above show the misfit surfaces produced by the demo_splitting_misfit example for the 0 degree polarisation angle. It is instructive to first consider the "simple" approach (lower left figure). This approach takes the average of the magnitude of the difference between the delay times and magnitude of the difference of between the fast directions. That is:

$\displaystyle{\frac{1}{2} \left(\frac{|dt_1-dt_2|}{(0.25/f_d)} + \frac{|\phi_1 - \phi_2|}{90}\right)}$,

where $f_d$, the dominant frequency, and 90 are included to properly normalise the two parts of the sum. This is not dependent on the initial polarisation direction and always forms a diamond shape with a minimum located at the point where $dt_1 = dt_2$ and $\phi_1 = \phi_2$. Another approach is the comparison of splitting intensity activated by the "intensity" method. The approach is to calculate the splitting intensity for both pairs of parameters:

$\displaystyle{S_i = dt_i \sin(2 \beta_i)}$,

(where $\beta$ is the difference between the initial polarisation angle and $\phi$) and taking the magnitude of the difference between $S_1$ and $S_2$. As shown in the lower right figure, the misfit surface is more complex but retains a minimum where the two splitting operators are equal. MSAT also implements two other approaches motivated by the way that SWS parameters can be extracted from data and, in particular the minimum eigenvalue method (Silver and Chan, 1991). Details of the approach, which involves splitting a probe wavelet using $\Gamma_1$, "unsplitting" it using $\Gamma_2$, and comparing the result with the probe wavelet, is given in the user guide but the result is shown in the top two figures. The top left figure shows the results of the "lam2" method which, because SWS operators are not commutative, differs if the values of $\Gamma_1$ and $\Gamma_2$ are exchanged. The top right figure shows the "lam2S" method where the forward and reversed "lam2" results are averaged to give a misfit function which is independent of the order that the splitting functions are supplied. The misfit function for both eigenvalue based methods change with both the initial polarisation angle and the dominant frequency of the test wavelet. In the following section the "lam2" misfit function is used to derive and elastic model that best fits SWS results.

The file examples/splitting_misfit/fit_TTI_orientation.m shows how the splitting misfit described above can be used to find an elastic model that matches a set of SWS measurements. In the following example an elastic model with tilted transverse anisotropy (TTI) is generated and used to calculate three splitting parameters that would correspond to observations of rays arriving from different azimuths and inclinations. A grid search over different orientations of the TTI medium is then performed and at each orientation the model’s predicted splitting parameters are calculated. These are then compared with the "observations" and the orientation that minimises the sum of the misfit found. This orientation is then reported (along with the resulting misfit surface. Key parts of the code for this example are described below

The first step is to generate an elasticity matrix describing the "observed" TTI medium and calculate the "observed" splitting parameters. The model is set up as follows:

and we note that (as is commonly the case for SWS) there is no way to distinguish a thin layer of strong anisotropy from a thick layer of weak anisotropy. We thus assume a 50 km thick layer of fixed strength of anisotropy throughout and only solve for the orientation of this layer. The "observed" parameters are returned by a the function call [fast,tlag,ravs]=create_dataset(Craw,rh,str,dip,razi,rinc,dist) ;, which makes use of MS_phasevels.

The second stage of the calculation is to compute the misfit between fast and tlag and the calculated splitting parameters for a range of TTI orientations. This is done in the loop over strikes and dips thus:

with the misfit stored in GMIS. Calculation of the misfit for each orientation is performed by the orientation_misfit function with the body of the calculation involving the use of MS_phasevels and MS_splitting_misfit for each "observed" splitting function:

The final step is to report and plot the best fitting model and misfit surface. The model and "observations" are plotted together using the "sdata" option in MS_plot:

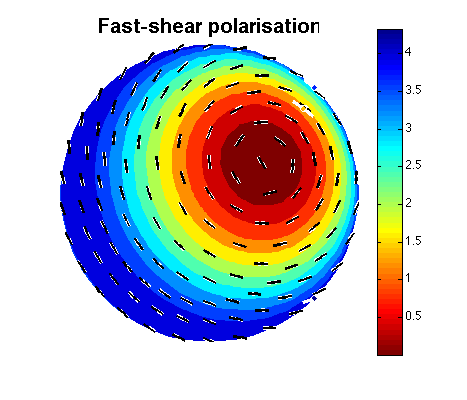
which produces the diagnostic pole figure below. In this figure "observed" SWS data (white lines, coloured spots refer to strength of anisotropy) and the best fitting model (black lines, coloured contours refer to strength of anisotropy) are both shown.