This example shows how to simulate the effect of a texture preserving phase transition (topotaxy) between MgSiO3 post-perovskite and MgSiO3 perovskite on increasing temperature or decreasing pressure in the lowermost mantle. Post-perovskite is assumed to deform by simple shear in its stability field and this is modelled using the VPSC code. The output of this modelling (a collection of Euler angles) is the input to this script. The Euler angles are first used to generate a model of the elasticity of textured post-perovskite just before the phase transition. A rotation matrix is built to describe the topotaxy and, together with the Euler angles, this is used to generate a model of the elasticity of the perovskite following the phase transition. Finally, a set of Euler angles representing the transformed perovskite is generated and these can be used to begin a further VPSC calculation of the deformation of pre-textured perovskite. This example is the program used to generate the results in Figure 2 of Dobson et al. (2013). Further information can be found in the supplementary information of that paper.

Note
MTEX and optional arguments

The example is packaged as a function taking a number of optional arguments to give the source of the VPSC output and restart files but these are not needed. The script can most simply be run as topotaxy_model() on the command line. The MTEX toolkit (Bachmann et al. 2010) can be used to produce pole figures of the textures but this is not required. The function can take one, two, or four optional arguments:

  • The first optional argument in the file name of a non-default input file to read the post-perovskite texture from. This defaults to "TEX_PH1.OUT" in the local directory.

  • The second is a file to be used to write the transformed perovskite texture in a format that can be read by the VPSC code. If no argument is provided no file is produced.

  • The third and fourth arguments allow the post-perovskite and perovskite elasticity to be written in a file for later reuse.

These can be used to examine how different assumptions for the active slip systems in perovskite and post-perovskite alter the results.

The code for this example can be found in /examples/topotaxy/topotaxy_model.m which, after parsing the optional arguments described above, performs a number of operations on the Euler angles read in from the input file.

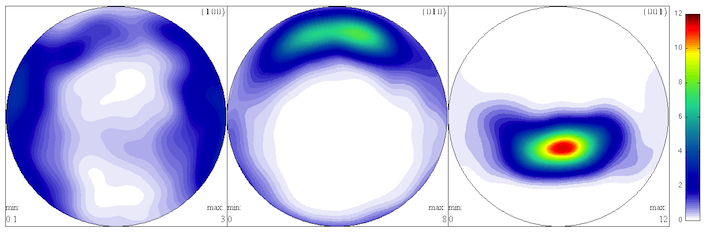
The input (post-perovskite) Euler angles are read into the array eulers using the included function read_VPSC_file(), which takes a file name as an argument. Pole figures of the input texture are shown below. These are only produced if MTEX is installed (see plot_pole_figure() for details.

Post-perovskite texture pole figures

The elasticity of the input polycrystalline aggregate can then be calculated using MS_rotEuler() and MS_VRH().

% Elasticity of textured ppv pre-transformeation
    Cs = zeros(6,6,nxtls);
    for i = 1:nxtls
        Cs(:,:,i) = MS_rotEuler(C_ppv, eulers(1,i), eulers(2,i), eulers(3,i));
    end
    rhos = ones(nxtls,1)*rh_ppv; % All crystals have the same density.
    vfs = ones(nxtls,1);         % Same volume fraction for each point
                                 % - normalised by MS_VRH.
    [C_ppv_av, rh_ppv_av] = MS_VRH(vfs, Cs, rhos);
    report_elasticity(C_ppv_av, rh_ppv_av, ...
        'post-perovskite before transformation');
    if write_elastic
        % Save Cij in format for reflectivity calc.
        MS_save(ppv_elastic_name, C_ppv_av, rh_ppv_av, 'Aij', 'eunit', ...
            'Pa');
    end

The function report_elasticity prints the resulting elasticity matrix and draws the phase velocity pole figures shown below.

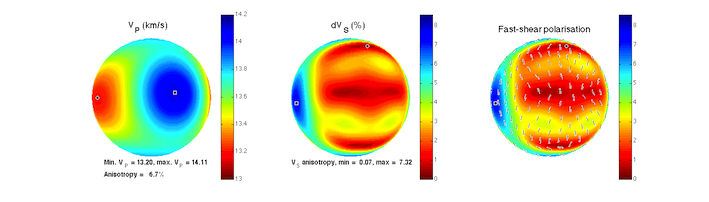
Post-perovskite phase velocities

Experiments suggest that the perovskite to post-perovskite phase transition exhibits topotaxy with the relations $[001]_{pv}=[001]_{ppv}$ and either $[100]_{pv}=[1\bar{1}0]_{ppv}$ or $[100]_{pv}=[110]_{ppv}$. This relationship is expressed as a rotation matrix by the function getTopotaxyRotations(), which calculates unit vectors along the crystallographic axes and then builds the rotation matrix to go from one to the other. For ease of manipulation the Euler angle triples describing the texture are also converted into rotation matrices using the rot_from_Euler() function:

function [ g ] = rot_from_Euler(phi1, theta, phi2)
    % Given three Euler angles phi1, Phi, phi2 (Bunge notation,
    % in degrees) return a rotation matrix, g, representing the
    % rotation. This is the 'passive' rotation.

    % Pre-compute trig functions.
    cp1 = cos(phi1*pi/180.0);
    sp1 = sin(phi1*pi/180.0);
    cp2 = cos(phi2*pi/180.0);
    sp2 = sin(phi2*pi/180.0);
    cth = cos(theta*pi/180.0);
    sth = sin(theta*pi/180.0);

    % Form rotation matrix for Bunge convention of
    % Euler angles, see eq 24 (pg81) of "Preferred
    % orientation in deformed meals and rocks... H-K Wenk (ed)"
    g = [cp1*cp2 - sp1*sp2*cth, sp1*cp2 + cp1*sp2*cth, sp2*sth ; ...
        -1*cp1*sp2 - sp1*cp2*cth, -1*sp1*sp2 + cp1*cp2*cth, cp2*sth; ...
        sp1*sth, -1*cp1*sth, cth];
end

This allows the Euler angles of the aggregate after the phase transition to be calculated:

    % Texture of transformed material
    % ===============================

        transformed_eulers = zeros(size(eulers));
        % Only do this if we need to for output or plotting
        for x = 1:nxtls
            if (chooser(x) < 0.5)
                g = rot_from_Euler(eulers(1,x), eulers(2,x), eulers(3,x));
                g = g*transA';
                [phi1, Phi, phi2] = rot_to_Euler(g);
            else
                g = rot_from_Euler(eulers(1,x), eulers(2,x), eulers(3,x));
                g = g*transB';
                [phi1, Phi, phi2] = rot_to_Euler(g);
            end
            transformed_eulers(1,x) = phi1;
            transformed_eulers(2,x) = Phi;
            transformed_eulers(3,x) = phi2;
        end

along with its elasticity. Pole figures for the transformed texture and phase velocity are shown below.

Perovskite texture pole figures

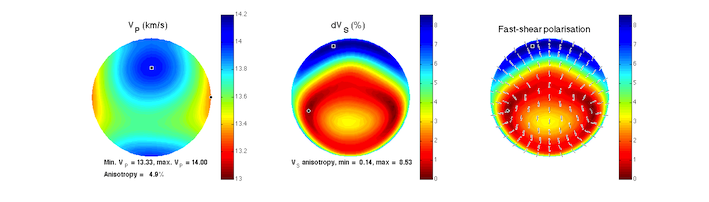
Perovskite phase velocities

The resulting texture and elasticity is then optionally written out for further use. The file /examples/topotaxy/extract_pv_def_results.m is a cut down version of the example described above which focuses on only the analysis of elasticity allowing the output perovskite texture to be further deformed using the VPSC code and the results examined.

References

  • D. P. Dobson, N. Miyajima, F. Nestola, M. Alvaro, N. Casati, C. Liebske, I. G. Wood and A. M. Walker (2013) "Strong texture inheritance between perovskite and post-perovskite in the D$^{\prime\prime}$ layer". Nature Geoscience. 10.1038/NGEO1844

  • F. Bachmann, R. Hielscher and H. Schaeben (2010) "Texture analysis with MTEX — free and open source software toolbox". Solid State Phenomena 160:63-68. 10.4028/www.scientific.net/SSP.160.63